分析方法与过程

1. 分析方法

在客户价值分析领域，最具有影响力并得到实证检验的理论与模型有：客户终生价值理论、客户价值金字塔模型、策略评估矩阵法和RFM客户价值分析模型等，其中应用最广泛的模型是RFM模型。其指标含义如下：

• R（Recency）指的是最近一次消费时间与截止时间的间隔。
• F（Frequency）指客户在某段时间内所消费的次数。
• M（Monetary）指客户在某段时间内所消费的金额。

在RFM模型理论中，最近一次消费时间与截止时间的间隔（R）、消费频率（F）、消费金额（M）是测算客户价值最重要的特征，这3个特征对营销活动具有十分重要的意义。其中，近一次消费时间与截止时间的间隔是最有力的特征。

（1）RFM模型结果解读

由于RFM模型包括3个特征，无法用平面坐标系来展示，所以这里使用三维坐标系进行展示，如下图所示，x轴表示R特征（Recency），y轴表示F特征（Frequency），z轴表示M指标（Monetary）。每个坐标轴一般会用5级表示程度，1为最小，5为最大。需要特别说明的是R特征：在x轴上，R值越大，代表该类客户最近一次消费与截止时间的消费间隔越短，客户R维度上的质量越好。

在每个轴上划分5个等级，等同于将客户划分成5×5×5=125种类型。这里划分为5级并不是严格的要求，一般是根据实际研究需求和客户的总量进行划分的，对于是否等分的问题取决于该维度上客户的分布规律。

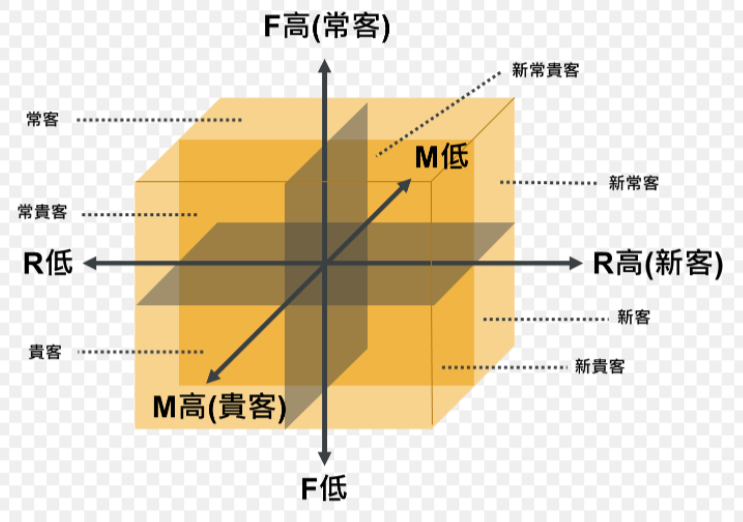
在上图中，左前上角方框的客户RFM特征取值为155。

• R值是比较小的，说明该类客户最近都没有来店消费，原因可能是最近比较忙，或者对现有的产品或服务不满意，或者是找到了更好的商家。R特征数值变小就需要企业管理人员引起重视，说明该类客户可能流失，会对企业造成损失。
• 消费频率F很高，说明客户很活跃，经常到商家店里消费。
• 消费金额M值很高，说明该类客户具备一定的消费能力，为店里贡献了很多的营业额。这类客户总体分析比较优质，但是R特征时间近度值较小，其往往是需要营销优化的客户群体。

同理，若客户RFM特征取值为555（右前上角）。则可以判定该客户为最优质客户，即这类客户最近到商家消费过，消费频率很高，消费金额很大。这类客户往往是企业利益的主要贡献者，需要重点关注与维护。

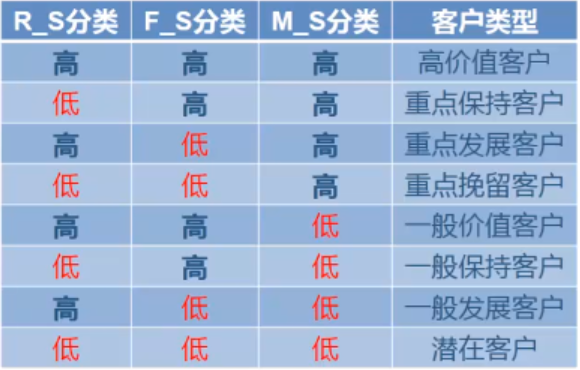
根据以上规律，可以把客户分成下表所示的不同发展对象来进行具体的分析。

 

（2）航空公司客户价值分析的LRFMC模型

在RFM模型中，消费金额表示在一段时间内客户购买该企业产品的金额的总和。由于航空票价受到运输距离、舱位等级等多种因素的影响，同样消费金额的不同旅客对航空公司的价值是不同的，例如，一位购买长航线、低等级舱位票的旅客与一位购买短航线、高等级舱位票的旅客相比，后者对于航空公司而言更有价值。因此这个特征并不适用于航空公司的客户价值分析。

本案例选择客户在一定时间内累积的飞行里程M和客户在一定时间内乘坐舱位所对应的折扣系数的平均值C两个特征代替消费金额。此外，航空公司会员入会时间的长短在一定程度上能够影响客户价值，所以在模型中增加客户关系长度L，作为区分客户的另一特征。

本案例将客户关系长度L、消费时间间隔R、消费频率F、飞行里程M和折扣系数的平均值C这5个特征作为航空公司识别客户价值的特征，记为LRFMC模型。其特征含义如下：

• L：会员入会时间距观测窗口结束的月数
• R：客户最近一次乘坐公司飞机距观测窗口结束的月数
• F：客户在观测窗口内乘坐公司飞机的次数
• M：客户在观测窗口内累计的飞行里程
• C：客户在观测窗口内乘坐舱位所对于的折扣系数的平均值

 

2. 分析步骤

• 抽取航空公司2012年4月1日至2014年3月31日的数据；
• 对抽取的数据进行数据探索分析与预处理，包括数据缺失值与异常值的探索分析、数据清洗、特征构建、标准化等操作；
• 基于RFM模型，使用K-Means算法进行客户分群；
• 针对模型结果得到不同价值的客户，采用不同的营销手段，提供定制化的服务。

 

3. 数据属性

数据存储于数据集“air_data.csv”中，其属性说明如下表所示：

	属性名称	属性说明
客户基本信息	MEMBER_NO	会员卡号
	FFP_DATE	入会时间(办理会员卡的开始时间)
	FIRST_FLIGHT_DATE	第一次飞行日期
	GENDER	性别
	FFP_TIER	会员卡级别
	WORK_CITY	工作地城市
	WORK_PROVINCE	工作地所在省份
	WORK_COUNTRY	工作地所在国家
	AGE	年龄
乘机信息	FLIGHT_COUNT	观测窗口内的飞行次数
	LOAD_TIME	观测窗口的结束时间(选取样本的时间宽度，距离现在最近的时间)
	LAST_TO_END	最后一次乘机时间至观测窗口结束时长
	AVG_DISCOUNT	平均折扣率
	SUM_YR	观测窗口的票价收入
	SEG_KM_SUM	观测窗口的总飞行公里数
	LAST_FLIGHT_DATE	末次飞行日期(最后一次飞行时间)
	AVG_INTERVAL	平均乘机时间间隔
	MAX_INTERVAL	最大乘机间隔
积分信息	EXCHANGE_COUNT	积分兑换次数
	EP_SUM	总精英积分
	PROMOPTIVE_SUM	促销积分
	PARTNER_SUM	合作伙伴积分
	POINTS_SUM	总累计积分
	POINT_NOTFLIGHT	非乘机的积分变动次数
	BP_SUM	总基本积分

 

项目一 数据探索分析

一、实验目标

• 通过对原始数据观察数据中是否存在票价为空值的记录，同时存在票价最小值为0、折扣率最小值为0但总飞行公里数大于0的异常记录；
• 选取客户基本信息中的入会时间、性别、会员卡级别和年龄字段进行探索分析，探索客户的基本信息分布情况；
• 选取入会时间、会员卡级别、客户年龄、飞行次数、总飞行公里数、最近一次乘机至结束时长、积分兑换次数、总累计积分属性，通过相关系数矩阵与热力图分析各属性间的相关性。

二、实验场所

线上/线下

三、实验设备与环境

电脑、VNC虚拟机、多媒体设备、Python、pycharm

四、实验要求

熟练掌握通过Python代码实现查找每列属性观测值中空值的个数、最大值、最小值等，且会绘制对应的可视化图表。

五、实验原理

通过编程实现对数据缺失值、异常值、数据分布和相关性进行分析。

六、实验内容

1. 1.数据抽取

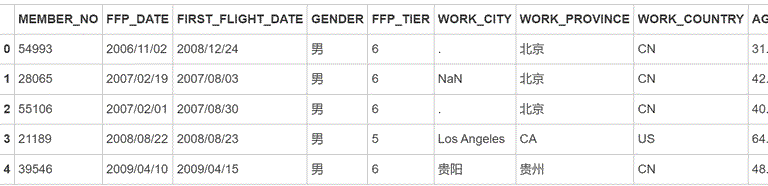
根据航空公司系统内的客户基本信息、乘机信息以及积分信息等详细数据，依据末次飞行日期(LAST_FLIGHT_DATE)，以及2014年3月31日未结束时间，选取宽度为两年的时间段作为分析观测窗口，抽取观测窗口2012年4月1日至2014年3月31日内有乘机记录的所有客户的详细数据形成历史数据，总共62988条记录。具体数据内容见数据集“air_data.csv”。

2. 2.查找每列属性观测值中空值个数、最大值、最小值

（1）读取数据并查看

import pandas as pd

data = pd.read_csv('../data/air_data.csv', encoding='utf-8')

data.head() 

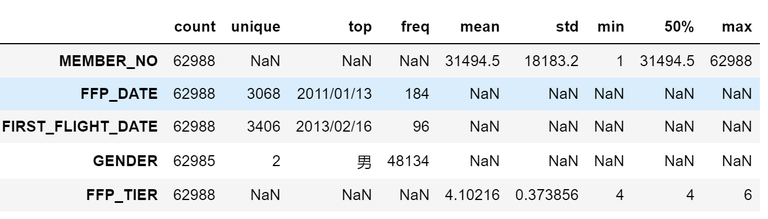
（2）缺失值分析

explore = data.describe( percentiles = [],include = 'all').T #对数据进行统计学估计，转置后便于观测

explore.head()

 

（3）找到每一个属性的空值、最大、最小值

#describe()函数自动计算非空值数，空值数需要手动计算

explore['null'] = len(data)-explore['count']

explore1 = explore[['null','max','min']]

explore1.columns = [u'空值数',u'最大值',u'最小值'] #重命名列名

explore1

打印结果见实验结果1中表格内容所示。

 

3．分布性分析

（1）客户基本信息分布分析

选取客户基本信息中的入会时间、性别、会员卡级别和年龄字段进行探索分析，探索客户的基本信息分布情况。

① 提取会员入会年份

from datetime import datetime

ffp = data['FFP_DATE'].apply(lambda x: datetime.strptime(x, '%Y/%m/%d'))

ffp_year = ffp.map(lambda x: x.year)

ffp_year

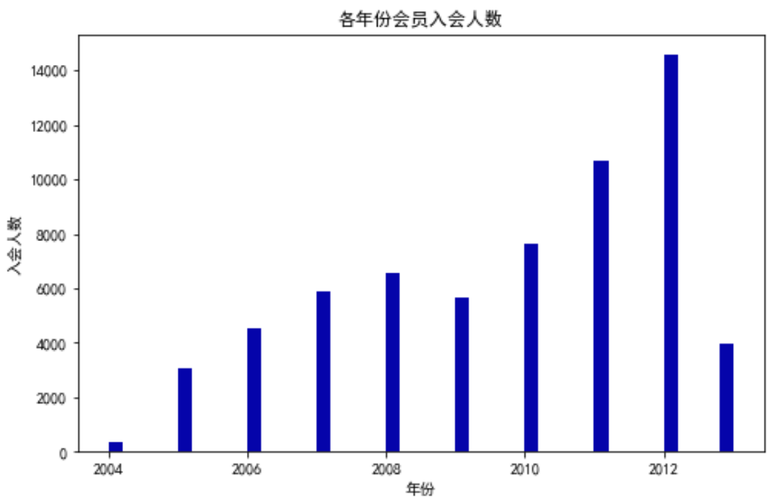
② 绘制各年份会员入会人数直方图

import matplotlib.pyplot as plt

%matplotlib inline

 

fig = plt.figure(figsize=(8, 5))  #设置画布大小

plt.rcParams['font.sans-serif'] = 'SimHei'  #运行配置参数中的字体（font）为黑体（SimHei）

plt.rcParams['axes.unicode_minus'] = False  #运行配置参数总的轴（axes）正常显示正负号（minus）

 

plt.hist(ffp_year, bins='auto', color='#0504aa')

plt.xlabel('年份')

plt.ylabel('入会人数')

plt.title('各年份会员入会人数')

plt.show()

 

③ 提取会员不同性别人数

male = pd.value_counts(data['GENDER'])['男']

female = pd.value_counts(data['GENDER'])['女']

 ④ 绘制会员性别比例图

fig = plt.figure(figsize=(7, 4))

plt.pie([male, female], labels=['男', '女'], colors=['lightskyblue', 'lightcoral'], autopct='%1.1f%%')

plt.title('会员性别比例')

plt.show()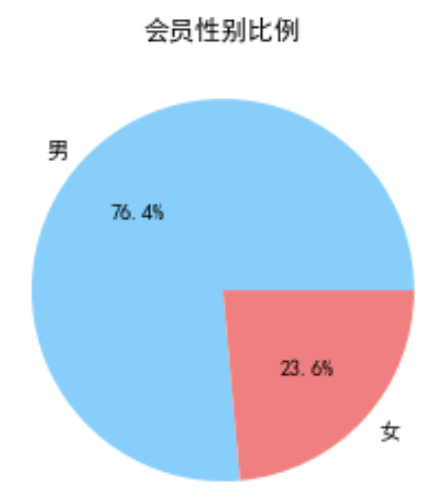

⑤ 提取不同级别会员的人数

lv_four = pd.value_counts(data['FFP_TIER'])[4]

lv_five = pd.value_counts(data['FFP_TIER'])[5]

lv_six = pd.value_counts(data['FFP_TIER'])[6]

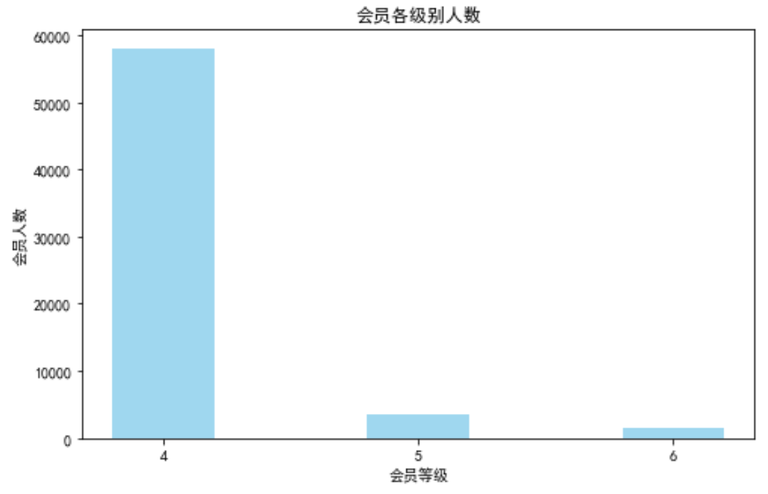
⑥ 绘制会员各级别人数的条形图

fig = plt.figure(figsize=(8, 5))

plt.bar(x=range(3), height=[lv_four, lv_five, lv_six], width=0.4, alpha=0.8, color='skyblue')

plt.xticks([index for index in range(3)], ['4', '5', '6'])

plt.xlabel('会员等级')

plt.ylabel('会员人数')

plt.title('会员各级别人数')

plt.show()

⑦ 提取会员年龄

age = data['AGE'].dropna()

age = age.astype('int64')

age

 

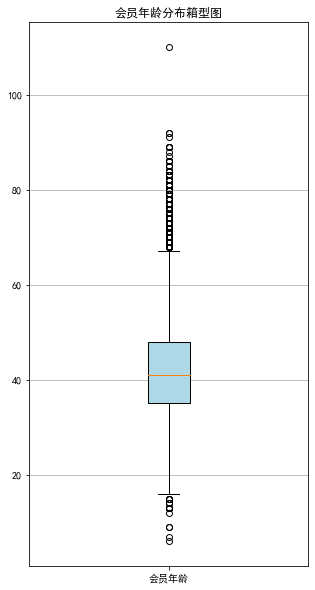
⑧ 绘制会员年龄分布箱型图

fig = plt.figure(figsize=(5, 10))

plt.boxplot(age, patch_artist=True, labels=['会员年龄'], boxprops={'facecolor':'lightblue'})

plt.title('会员年龄分布箱型图')

plt.grid(axis='y')  #显示y坐标轴的底线

plt.show()

 

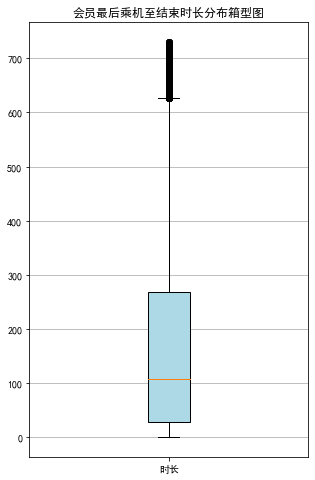
（2）客户乘机信息分布分析

选取最后一次乘机至结束的时长、客户乘机信息中的飞行次数、总飞行公里数进行探索分析，探索客户的乘机信息分布情况。

① 绘制最后乘机至结束时长箱型图

lte = data['LAST_TO_END']

fc = data['FLIGHT_COUNT']

skc = data['SEG_KM_SUM']

#绘制最后乘机至结束时长箱型图

fig = plt.figure(figsize=(5, 8))

plt.boxplot(lte, patch_artist=True, labels=['时长'], boxprops={'facecolor': 'lightblue'})

plt.title('会员最后乘机至结束时长分布箱型图')

plt.grid(axis='y')

plt.show()

 

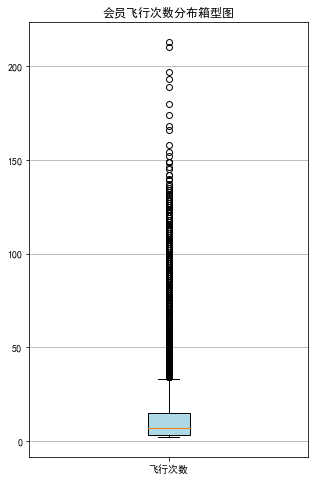
② 绘制客户飞行次数箱型图

fig = plt.figure(figsize=(5, 8))

plt.boxplot(fc, patch_artist=True, labels=['飞行次数'], boxprops={'facecolor': 'lightblue'})

plt.title('会员飞行次数分布箱型图')

plt.grid(axis='y')

plt.show()

 

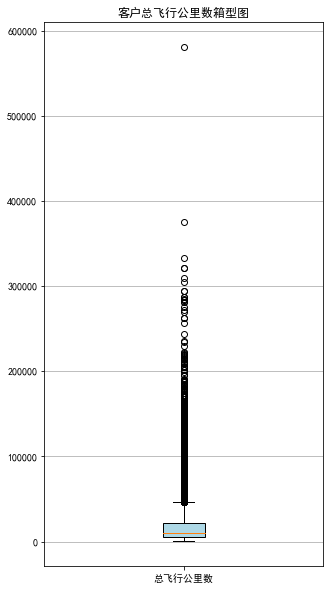
③ 绘制客户总飞行公里数箱型图

fig = plt.figure(figsize=(5, 10))

plt.boxplot(skc, patch_artist=True, labels=['总飞行公里数'], boxprops={'facecolor': 'lightblue'})

plt.title('客户总飞行公里数箱型图')

plt.grid(axis='y')

plt.show()

 

 

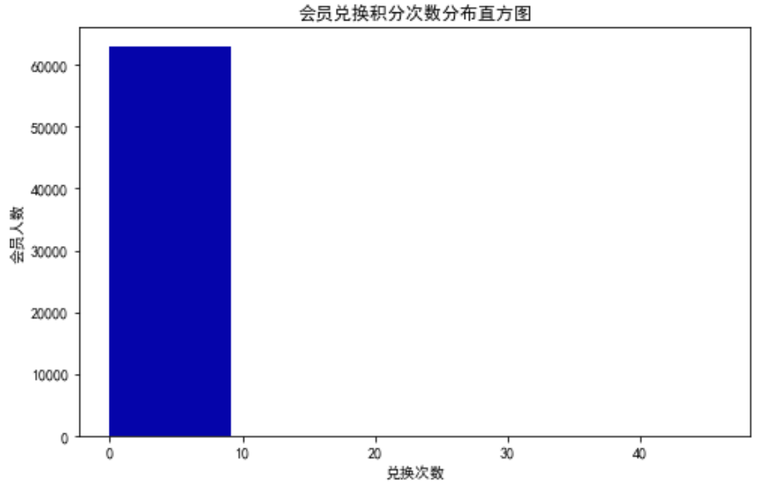
（3）客户积分信息分布分析

选取积分兑换次数、总累计积分进行探索分析，探索客户的积分信息分布情况。

① 提取会员积分兑换次数

ec = data['EXCHANGE_COUNT']

ec 

② 绘制会员兑换积分次数直方图

fig = plt.figure(figsize=(8, 5))

plt.hist(ec, bins=5, color='#0504aa')

plt.xlabel('兑换次数')

plt.ylabel('会员人数')

plt.title('会员兑换积分次数分布直方图')

plt.show()

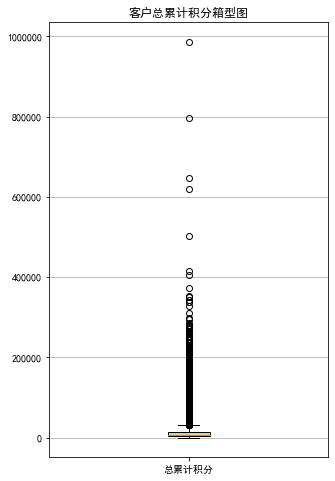
③ 提取会员总累计积分，并绘制会员总累计积分箱型图

#提取会员总累计积分

ps = data['Points_Sum']

#绘制会员总累计积分箱型图

fig = plt.figure(figsize=(5, 8))

plt.boxplot(ps, patch_artist=True, labels=['总累计积分'], boxprops={'facecolor': 'lightblue'})

plt.title('客户总累计积分箱型图')

plt.grid(axis='y')

plt.show()

 

 

4．相关性分析

客户信息属性之间存在相关性，选取入会时间、会员卡级别、客户年龄、飞行次数、总飞行公里数、最近一次乘机至结束时长、积分兑换次数、总累计积分属性，可通过相关系数矩阵与热力图分析各属性间的相关性。

（1）提取属性并合并为新数据集

data_corr = data[['FFP_TIER', 'FLIGHT_COUNT', 'LAST_TO_END', 'SEG_KM_SUM', 'EXCHANGE_COUNT', 'Points_Sum']]

age1 = data['AGE'].fillna(0)

data_corr['AGE'] = age1.astype('int64')

data_corr['ffp_year'] = ffp_year

 

（2）计算相关性矩阵

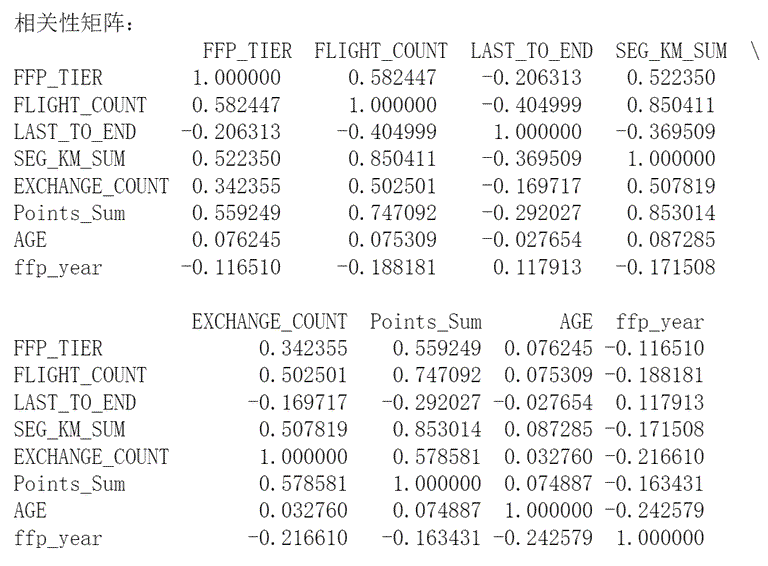
dt_corr = data_corr.corr(method='pearson')

print('相关性矩阵：\n', dt_corr)

 

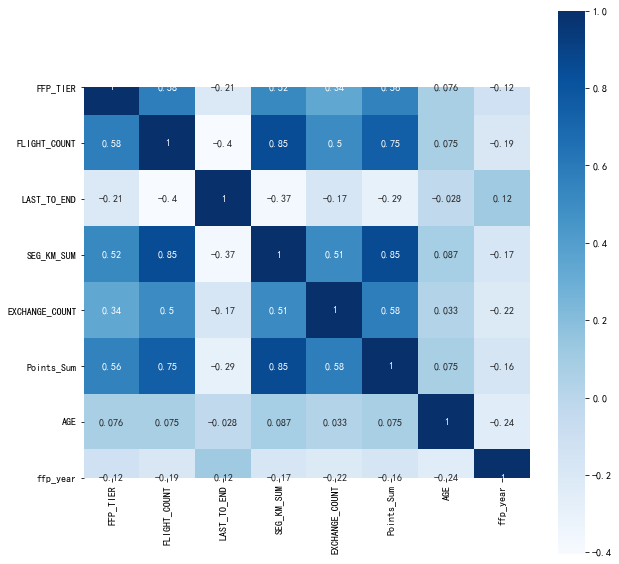
（3）绘制热力图

import seaborn as sns

plt.subplots(figsize=(10, 10))

sns.heatmap(dt_corr, annot=True, vmax=1, square=True, cmap='Blues')

plt.show()

 

七、实验结果

1. 通过对原始数据观察发现数据中存在票价为空值的记录，同时存在票价最小值为0、折扣率最小值为0但总飞行公里数大于0的记录。

表1 查找每列属性观测值中空值个数、最大值、最小值

	空值数	最大值	最小值
MEMBER_NO	0	62988	1
FFP_DATE	0	NaN	NaN
FIRST_FLIGHT_DATE	0	NaN	NaN
GENDER	3	NaN	NaN
FFP_TIER	0	6	4
WORK_CITY	2269	NaN	NaN
WORK_PROVINCE	3248	NaN	NaN
WORK_COUNTRY	26	NaN	NaN
AGE	420	110	6
LOAD_TIME	0	NaN	NaN
FLIGHT_COUNT	0	213	2
BP_SUM	0	505308	0
EP_SUM_YR_1	0	0	0
EP_SUM_YR_2	0	74460	0
SUM_YR_1	551	239560	0
SUM_YR_2	138	234188	0
SEG_KM_SUM	0	580717	368
WEIGHTED_SEG_KM	0	558440	0
LAST_FLIGHT_DATE	0	NaN	NaN
AVG_FLIGHT_COUNT	0	26.625	0.25
AVG_BP_SUM	0	63163.5	0
BEGIN_TO_FIRST	0	729	0
LAST_TO_END	0	731	1
AVG_INTERVAL	0	728	0
MAX_INTERVAL	0	728	0
ADD_POINTS_SUM_YR_1	0	600000	0
ADD_POINTS_SUM_YR_2	0	728282	0
EXCHANGE_COUNT	0	46	0
avg_discount	0	1.5	0
P1Y_Flight_Count	0	118	0
L1Y_Flight_Count	0	111	0
P1Y_BP_SUM	0	246197	0
L1Y_BP_SUM	0	259111	0
EP_SUM	0	74460	0
ADD_Point_SUM	0	984938	0
Eli_Add_Point_Sum	0	984938	0
L1Y_ELi_Add_Points	0	728282	0
Points_Sum	0	985572	0
L1Y_Points_Sum	0	728282	0
Ration_L1Y_Flight_Count	0	1	0
Ration_P1Y_Flight_Count	0	1	0
Ration_P1Y_BPS	0	0.999989	0
Ration_L1Y_BPS	0	0.999993	0
Point_NotFlight	0	140	0

• 票价为空值，可能是不存在飞行记录（即客户不存在乘机记录）；
• 其他空值可能是，飞机票来自于积分兑换等渠道。查找每列属性观测值中空值的个数、最大值、最小值。

 

2. 分布分析实验结果见3中各子节描述。
3. 分布分析实验结果见3中各子节描述。

项目二  数据预处理

一、实验目标

本案例主要采用数据清洗、属性规约与数据变换的预处理方法对数据进行预处理。

二、实验场所

线上/线下

三、实验设备与环境

电脑、VNC虚拟机、多媒体设备、Python、pycharm

四、实验要求

熟练掌握数据预处理之数据清理、属性规约、数据变换相关知识，通过代码实现对数据的预处理操作。

五、实验原理

使用pandas对满足清洗条件的数据进行丢弃，即对满足条件的一行数据全部丢弃；删除冗余信息，并统一数据格式。

六、实验内容

1.数据清洗

通过项目一种分析，观察数据发现，原始数据中存在票价为空值、票价最小值为0、折扣率最小值为0、总飞行公里数大于0的记录。票价为空值的数据可能是客户不存在乘机记录造成的。其他的数据可能是客户乘坐0折机票或者积分兑换造成的。

由于原始数据量大，这类数据所占比例较小，对于问题影响不大，因此对其进行丢弃处理。同时，在进行数据探索时，发现部分年龄大于100的记录，也进行丢弃处理。具体处理方法如下：

• 丢弃票价为空的记录；
• 保留票价不为0的，或者平均折扣率不为0且飞行公里数大于0的记录；
• 丢弃年龄大于100的记录。

（1）查看原始数据的形状

import numpy as np

import pandas as pd

 

datafile = '../data/air_data.csv'  #原始数据路径

cleanedfile = '../data/data_cleaned.csv'  #数据清洗后的保存路径

 

airline_data = pd.read_csv(datafile, encoding='utf-8')

print('原始数据的形状：', airline_data.shape)

 

（2）去除票价为空的记录

airline_notnull = airline_data.loc[airline_data['SUM_YR_1'].notnull() & airline_data['SUM_YR_2'].notnull(), :]

print('删除缺失记录后数据的形状为：', airline_notnull.shape)

 

（3）只保留票价非零的，或者平均折扣率不为0且与总飞行公里数大于0的记录

index1 = airline_notnull['SUM_YR_1'] != 0

index2 = airline_notnull['SUM_YR_2'] != 0

index3 = (airline_notnull['SEG_KM_SUM'] > 0) & (airline_notnull['avg_discount'] != 0)

index4 = airline_notnull['AGE'] > 100  #去除年龄大于100的记录

 

airline = airline_notnull[(index1 | index2) & index3 & -index4]

print('经过清洗后的数据的形状为：', airline.shape)

 

airline.to_csv(cleanedfile)  #保存清洗后的数据

 

 

2. 2.属性规约

原始数据中属性太多，根据航空公司客户价值LRFMC模型，选择与LRFMC指标相关的6个属性：FFP_DATE、LOAD_TIME、FLIGHT_COUNT、AVG_DISCOUNT、SEG_KM_SUM、LAST_TO_END。删除与其不相关、弱相关或冗余的属性，如会员卡号、性别、工作地城市、工作地所在省份、工作地所在国家、年龄等属性。

import pandas as pd

import numpy as np

#读取清洗后的数据

cleanedfile = '../data/data_cleaned.csv'  #数据清洗后的保存路径

airline = pd.read_csv(cleanedfile, encoding='utf-8')

#选取需求属性

airline_selection = airline[['LOAD_TIME','FFP_DATE','LAST_TO_END','FLIGHT_COUNT','SEG_KM_SUM','avg_discount']]

print('筛选的属性前5行为：')

airline_selection.head()

 

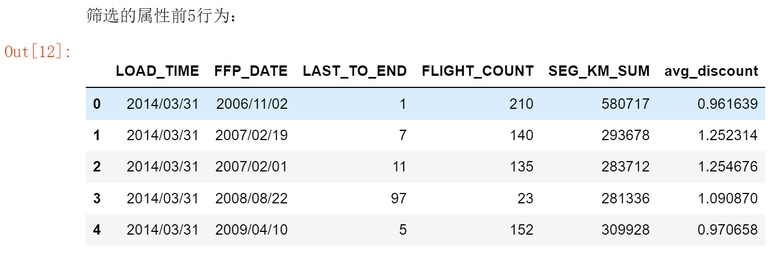
3. 3.数据变换

数据变换是将数据变换成“适当的”格式，以适应挖掘任务及算法的需求。本案例中主要采用属性构造和数据标准化的数据变换方式。

（1）构造属性

from datetime import datetime

 

airline_selection['L1'] = pd.to_datetime(airline_selection['LOAD_TIME']) - pd.to_datetime(airline_selection['FFP_DATE'])

L = []

for i in airline_selection['L1']:

    a = int(str(i)[:4])/30

    L.append(a)

airline_selection['L'] = L

airline_selection.drop('L1', axis=1, inplace =True) # 删除中间变量

airline_selection.drop(airline_selection.columns[:2], axis=1, inplace =True) 

# 去掉不需要的u'LOAD_TIME', u'FFP_DATE'

airline_selection.rename(columns={'LAST_TO_END':'R','FLIGHT_COUNT':'F','SEG_KM_SUM':'M','avg_discount':'C'},inplace=True)

airline_selection.head()

 

 

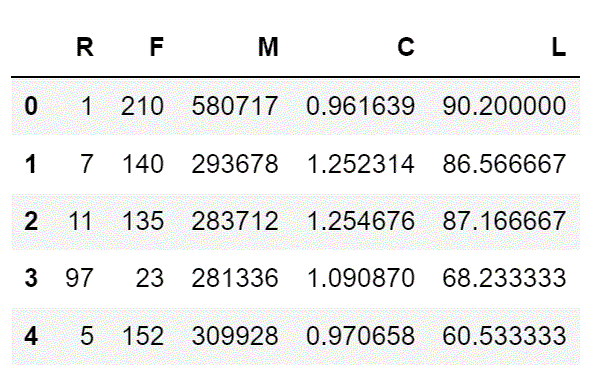
（2）查看5个指标的取值范围

def f(x):

    return pd.Series([x.min(),x.max()], index=['min','max'])

d = airline_selection.apply(f)

d

 

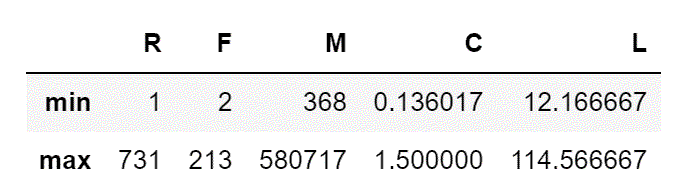
从结果来看，5个指标的取值范围数据差异较大，为了消除数量级数据带来的影响，需要对数据进行标准化处理。

（3）标准化处理

from sklearn.preprocessing import StandardScaler

data = StandardScaler().fit_transform(airline_selection)

 

data = StandardScaler().fit_transform(airline_selection)

data = pd.DataFrame(data)

data.columns = ['Z' + i for i in airline_selection.columns]

data =data.iloc[:,[4,0,1,2,3]]   # 列进行排序

np.savez('../data/airline_scale.npz', data)

data.head()

 

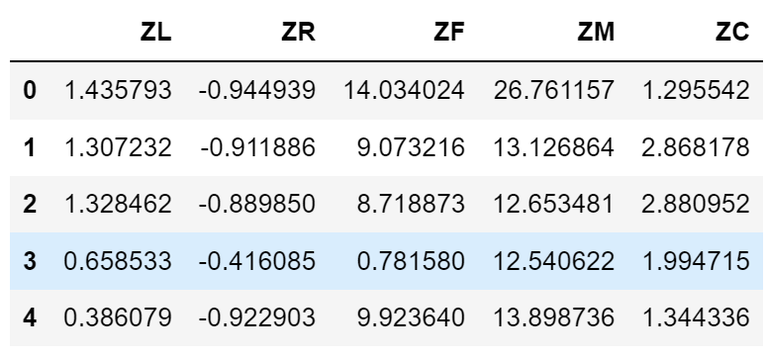
七、实验结果

    实验结果见实验内容代码后截图。

项目三  模型构建

一、实验目标

采用K-Means聚类算法对客户数据进行客户分群，并根据聚类结果绘制客户分群雷达图，从而通过比较各个特征在群间的大小来对某一个群的特征进行评价分析。

二、实验场所

线上/线下

三、实验设备与环境

电脑、VNC虚拟机、多媒体设备、Python、pycharm

四、实验要求

熟练使用K-Means聚类算法实现对客户数据的分群；通过Python编程实现数据可视化，实现对客户的价值分析，针对聚类结果进行特征分析。

五、实验原理

客户价值分析模型构建主要由两个部分构成：

• 根据航空公司客户5个指标的数据，对客户作K-means聚类分群；
• 结合业务对每个客户群进行特征分析，绘制雷达图分析其客户价值，并对每个客户群进行排名。

六、实验内容

1. 1.客户聚类

采用K-Means聚类算法对客户数据进行客户分群，聚成5类。

import pandas as pd

import numpy as np

from sklearn.cluster import KMeans

#读取标准化后的数据

airline_scale = np.load('../data/airline_scale.npz')['arr_0']

k = 5  #确定聚类中心数

#构建模型，随机种子设为123

kmeans_model = KMeans(n_clusters=k,random_state=123) 

fit_kmeans = kmeans_model.fit(airline_scale)  #模型训练

 

（1）查看聚类结果

kmeans_cc = kmeans_model.cluster_centers_  #聚类中心

print('各聚类中心为：\n', kmeans_cc)

 

（2）样本的类别标签

kmeans_labels = kmeans_model.labels_  #样本的类别标签

print('各样本的类别标签为：\n', kmeans_labels)

 

（3）统计不同类别样本的数目

r1 = pd.Series(kmeans_model.labels_).value_counts()  #统计不同类别样本的数目

print('最终每个类别的数目为：\n', r1)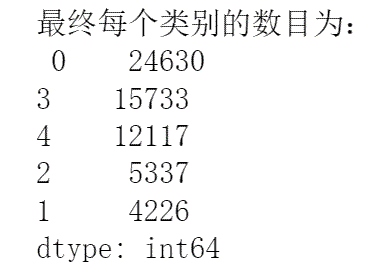 

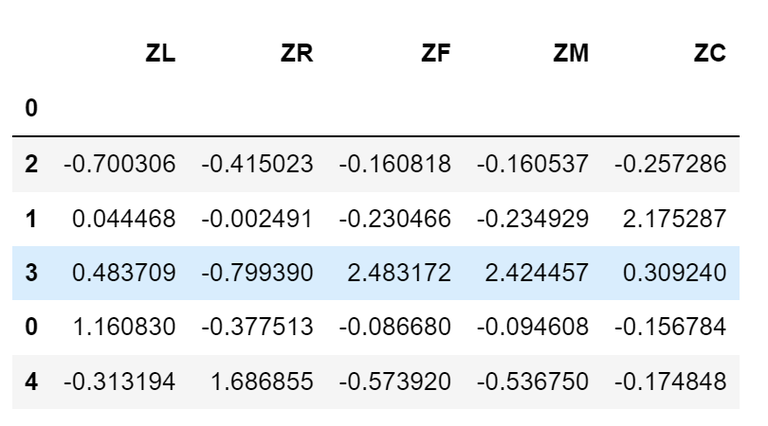
（4）输出聚类分群的结果

cluster_center = pd.DataFrame(kmeans_model.cluster_centers_, columns=['ZL', 'ZR', 'ZF', 'ZM', 'ZC'])  #将聚类中心放在数据框中

cluster_center.index = pd.DataFrame(kmeans_model.labels_).drop_duplicates().iloc[:, 0]  #将样本类别作为数据框索引

cluster_center

 

2. 2.客户价值分析

针对聚类结果进行特征分析，绘制客户分群雷达图。

%matplotlib inline

import matplotlib.pyplot as plt

 

# 客户分群雷达图

labels = ['ZL','ZR','ZF','ZM','ZC']

legen = ['客户群' + str(i + 1) for i in cluster_center.index] #客户群命名

lstype = ['-','--',(0, (3, 5, 1, 5, 1, 5)),':','-.']

kinds = list(cluster_center.iloc[:, 0])

# 由于雷达图要保证数据闭合，因此再添加L列，并转换为np.ndarray

cluster_center = pd.concat([cluster_center, cluster_center[['ZL']]], axis=1)

centers = np.array(cluster_center.iloc[:, 0:])

 

# 分割圆周长

n = len(labels)

angle = np.linspace(0, 2 * np.pi, n, endpoint=False)

#angle = np.concatenate((angle, [angle[0]]))  #并让其闭合

 

# 绘图

fig = plt.figure(figsize=(8,6))

ax = fig.add_subplot(111, polar=True)                # 以极坐标的形式绘制图形

plt.rcParams['font.sans-serif'] = ['SimHei']         # 用来正常显示中文标签

plt.rcParams['axes.unicode_minus'] = False           # 用来正常显示负号

 

# 画线

for i in range(len(kinds)):

ax.plot(angle, centers[i], linestyle=lstype[i], linewidth=2, label=kinds[i])

 

# 添加属性标签

angle = np.linspace(0, 2 * np.pi, n, endpoint=False)

ax.set_thetagrids(angle * 180 / np.pi, labels)

plt.title('客户特征分析雷达图')

plt.legend(legen)

plt.show()

绘制的雷达图见实验结果所示图表。

七、实验结果

 

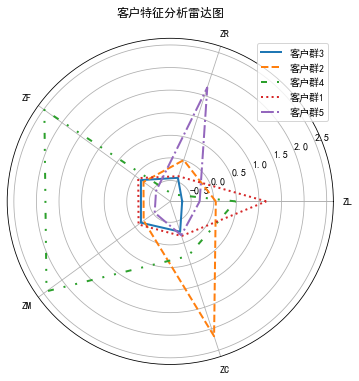
    结合业务分析，通过比较各个特征在群间的大小来对某一个群的特征进行评价分析——

• 客户群1：在特征C处的值最大，在特征F、M处的值较小，说明客户群1是偏好乘坐高级舱位的客户群；
• 客户群2：在特征F和M上的值最大，且在特征R上的值最小，说明客户群2的会员频繁乘机且最近都有乘机记录；
• 客户群3：在特征R处值最大，在其他特征处的值都较小，说明客户群3已经很久没有乘坐飞机，是入会时间短的低价值的客户群；
• 客户群4：在所有特征上的值都较小，且特征L处的值最小，说明客户群4属于新入会员较多的客户群；
• 客户群5：在特征L处的值最大，在特征R处的值最小，其他都比较适中，说明客户群5入会时间长，飞行频率也较高，是有较高价值的客户。