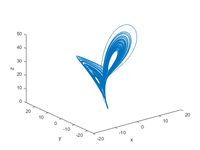
非线性系统可视化
项目背景
(1)混沌理论
混沌理论(Chaos theory)是关于非线性系统在一定参数条件下展现分岔(bifurcation)、周期运动与非周期运动相互纠缠,以至于通向某种非周期有序运动的理论。在耗散系统和保守系统中,混沌运动有不同表现,前者有吸引子,后者无(也称含混吸引子)。
从20世纪80年代中期到20世纪末,混沌理论迅速吸引了数学、物理、工程、生态学、经济学、气象学、情报学等诸多领域学者有关注,引发了全球混沌热。混沌,也写作混沌(比如《庄子》)。自然科学中讲的混沌运动指确定性系统中展示的一种貌似随机的行为或性态。确定性(deterministic)是指方程不含随机项的系统,也称动力系统(dynamical system)。典型的模型有单峰映象(logistic map)迭代系统,洛伦兹微分方程系统,若斯叻吸引子,杜芬方程,蔡氏电路,Chen 吸引子等。为混沌理论做出重要贡献的学者有庞加莱、洛伦兹、上田睆亮(Y. Ueda)、费根堡姆、约克、李天岩、斯美尔、芒德勃罗和郝柏林等。混沌理论向前可追溯到19世纪庞加莱等人对天体力学的研究,他提出了同宿轨道、异宿轨道的概念,他也被称为混沌学之父。
混沌行为可以在许多自然系统中被观测到,例如天气和气候。对于这个行为的研究,可以通过分析混沌数学模型,或者通过诸如递归图和庞加莱映射等分析技术。
混沌理论在许多科学学科中得到广泛应用,包括:数学、生物学、信息技术、经济学、工程学、金融学、哲学、物理学、政治学、人口学、心理学和机器人学。
多种系统的混沌状态在实验室中得到观察,包括电路、激光、流体的动态,以及机械和电磁装置。在自然中进行的有对天气、卫星运动、天体磁场、生态学中的种群增长、神经元中的动作电位和分子振动的观察。
混沌理论最成功的应用之一在于生态学中的雷克动态综合模型,在其中显示了受密度制约之下的种群增长如何引致混沌状态。
(2)蝴蝶效应产生背景
在1972年12月29日,美国麻省理工教授、混沌学开创人之一E.N.洛仑兹在美国科学发展学会第139次会议上发表了题为《蝴蝶效应》的论文,提出一个貌似荒谬的论断:在巴西一只蝴蝶翅膀的拍打能在美国得克萨斯州产生一个龙卷风,并由此提出了天气的不可确预报性。至此以后,人们对于混沌学研究的兴趣十分浓厚。
美国气象学家洛伦兹(E.N.Lorenz,不要和提出洛伦兹变换的那位搞混)是混沌理论的奠基者之一。20世纪50年代末到60年代初,他的主要工作目标是从理论上进行长期天气预报研究。他在使用计算机模拟天气时意外发现,对于天气系统,哪怕初始条件的微小改变也会显著影响运算结果。随后,他在同事工作的基础上化简了自己先前的模型,得到了有3个变量的一阶微分方程组,由它描述的运动中存在一个奇异吸引子,即洛伦兹吸引子。
洛伦兹的工作结果最初在1963年发表,论文题目为Deterministic Nonperiodic Flow,发表在Journal of the Atmospheric Sciences杂志上。如今,这一方程组已成为混沌理论的经典,也是“巴西蝴蝶扇动翅膀在美国引起德克萨斯的飓风”一说的肇始。它的形式看起来很简单:
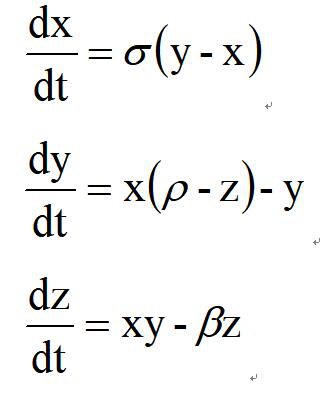
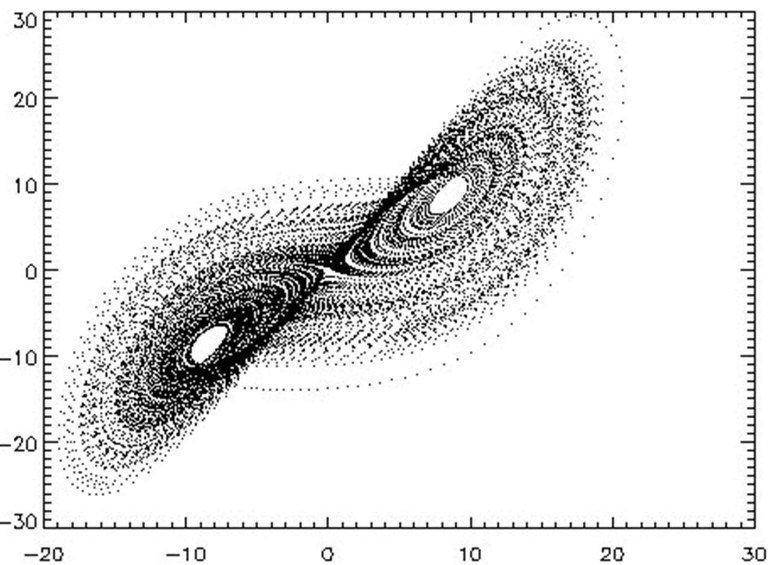
洛伦兹方程组是基于流体力学中的Navier-Stokes方程、热传导方程和连续性方程构建的,属于耗散系统。相空间中,耗散系统的终态都将收缩到吸引子的状态上。但对平庸吸引子来说,无论初值如何,终值只有一个,而奇异吸引子却是无数个点的集合,对初值极端敏感。如洛伦兹当年只是忽略了小数点4位以后的数值,得到的结果就有了相当大的偏差,甚至是完全相反。在洛仑兹原始的工作中,x表示的是对流的翻动速率,y正比于上流与下流液体温差,z是垂直方向的温度梯度。式中三个参数 σ(Prandtl数)、 ρ和 β(Rayleigh数)可任取大于0的数值。常用的组合是 σ=10,β=8/3 ,而令ρ 取不同数值。 ρ=28时有混沌现象,奇异吸引子出现,此时系统的演化轨迹如下图所示:
项目描述
(1)弄懂什么是非线性系统,包括非线性系统的概念、特点、发展历程;
(2)了解非线性系统的特征及相关指标;
(3)学习非线性系统的数值计算方法,重点学习龙格库塔算法的原理;
(4)通过Python编程实现洛伦兹混沌系统的仿真,并用动图的方式给出演示结果。
项目功能
本次项目的目的是为了让学生掌握利用Python实现非线性系统的可视化。
项目展示
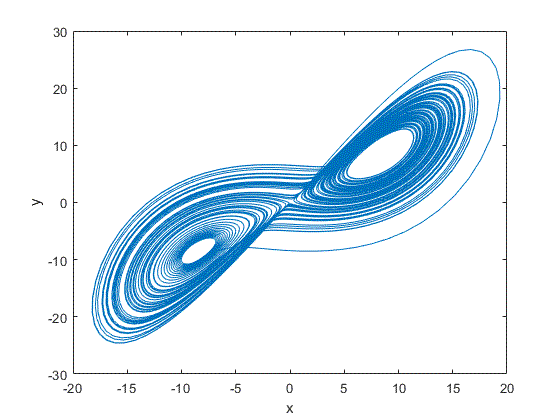
对利用Python得到的动图进行截图如下所示:
(1)二维
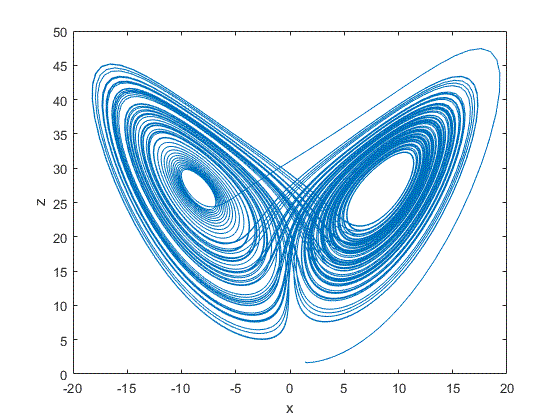
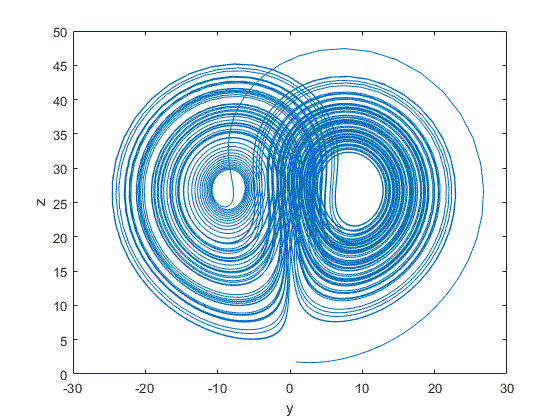
(2)三维
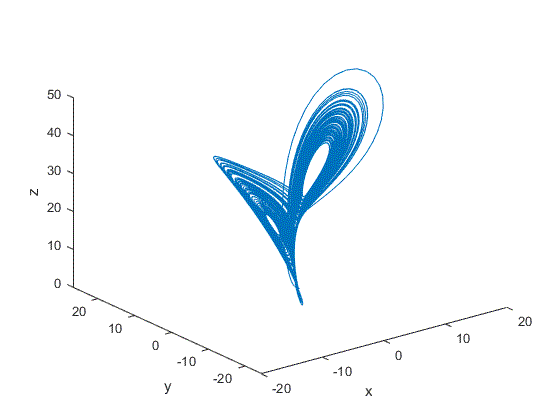
对应主要代码部分如下所示:
if __name__=='__main__':
h = 0.01
FinalTime = 100
t = np.linspace(0, FinalTime, math.floor(FinalTime/h)+1, endpoint=True)
N = len(t)
X = [1.4443, 0.8667, 1.7614]
Y = []
Y.append(X)
for n in range(1,N):
k1 = h*np.asarray(fx(X))
k2 = h*np.asarray(fx(X+k1/2))
k3 = h*np.asarray(fx(X+k2/2))
k4 = h*np.asarray(fx(X+k3))
X = X + (k1+2*k2+2*k3+k4)/6
Y.append(X)
Z = np.array(Y)
fig, ax = plt.subplots()
xdata, ydata = [], []
ln, = plt.plot([], [], 'blue', linewidth=0.5, animated=True)
def init():
ax.set_xlim(-20, 20)
ax.set_ylim(0, 50)
plt.title("Lorenz System")
plt.xlabel("x")
plt.ylabel("z")
return ln,
def update(frame):
xdata.append(Z[5*frame, 0])
ydata.append(Z[5*frame, 2])
xdata.append(Z[5*frame+1, 0])
ydata.append(Z[5*frame+1, 2])
xdata.append(Z[5*frame+2, 0])
ydata.append(Z[5*frame+2, 2])
xdata.append(Z[5*frame+3, 0])
ydata.append(Z[5*frame+3, 2])
xdata.append(Z[5*frame+4, 0])
ydata.append(Z[5*frame+4, 2])
ln.set_data(xdata, ydata)
return ln,